Coloration de graphes simples non orientés¶

Comme aux TP précédents, nous aurons besoin de numpy et de certaines de vos fonctions du TP1.

In [2]:
import numpy as np
from graph import *

Les graphes manipulés ici seront des 1-graphes non orientés, connexes et sans boucles.

1. Coloration de sommets¶

Problèmatique :
Un problème de coloration consiste à affecter une couleur à chaque sommet d'un graphe de sorte que deux sommets voisins soient de couleurs différentes. L'objectif est de minimiser le nombre de couleurs utilisées.

1.1 Attribut color¶

Supposons g, un graphe à n sommets. La classe Graphpossède un attribut color, qui est une liste de nentiers. Au moment de l'affichage grâce à la méthode g.display(), chaque entier de la liste g.color est associé à une couleur.

Exemple :

In [3]:
g = Graph(directed=False)
g.successors = {0:{1,2,4,5},
                1:{0,2,3},
                2:{1,0,5},
                3:{1},
                4:{0},
                5:{0,2}}

# par défaut, l'attribut color est une liste vide. Les sommets du graphe sont alors blancs
print("la liste des couleurs est :",g.color)
g.display()

la liste des couleurs est : []
Out[3]:
G G 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5
In [4]:
liste_couleur = [5,2,2,1,7,4]
g.color = liste_couleur
print("la liste des couleurs est :",g.color)
g.display()

la liste des couleurs est : [5, 2, 2, 1, 7, 4]
Out[4]:
G G 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5

Explication :

  • Le sommet 0 reçoit liste_couleur[0], à savoir l'entier 5 à qui la méthode display() associe le bleu.
  • Le sommet 1 reçoit liste_couleur[1], à savoir l'entier 2 qui est associé au vert.
  • Le sommet 2 reçoit liste_couleur[2], à savoir lui aussi l'entier 2 qui est associé au vert.
  • Le sommet 3 reçoit liste_couleur[3], à savoir l'entier 1 qui est associé au orange.
  • Le sommet 4 reçoit liste_couleur[4], à savoir l'entier 7 qui est associé au magenta.
  • Le sommet 5 reçoit liste_couleur[5], à savoir l'entier 4 qui est associé au cyan.

Attention !!
Un même entier ne sera pas toujours associé à la même couleur dans deux graphes différents !

Mais le plus grand entier donné sera toujours associé au magenta, les autres couleurs établissant une correspondance entre entiers et positions sur le spectre lumineux.

Le nombre 0 correpond lui au blanc : on l'utilisera comme absence de couleur.

In [5]:
g.color= [5,0,2,1,15,4]
print("la liste des couleurs est :",g.color)
g.display()

la liste des couleurs est : [5, 0, 2, 1, 15, 4]
Out[5]:
G G 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5

1.2 Exercices de coloration¶

1.2.1 Exercice 1¶

  • Construire une fonction exo1(g,sommets) qui colorie le graphe gde la façon suivante :
    • affecter des couleurs distinctes (et non blanches) aux sommets donnés en paramètres.
    • colorer en blanc les autres sommets.

Exemple :

In [7]:
exo1(g,[0,2,4])
g.display()
Out[7]:
G G 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5

1.2.2 Exercice 2¶

  • Construire une fonction exo2(g,x)qui qui colorie le graphe gde la façon suivante :
    • colorer le sommet x, ainsi que ses voisins, avec une couleur (non blanche) différente pour chaque.
    • colorer les autres sommets en blanc.

Exemple :

In [9]:
exo2(g,2)
g.display()
Out[9]:
G G 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5

1.2.3 Exercice 3¶

  • Construire une fonction exo3(g)qui qui colorie le graphe gde la façon suivante :
    • colorer en une couleur le(s) sommet(s) de plus haut degré, et en une autre couleur celui(/ceux) de plus bas degré.
    • colorer les autres sommets en blanc.

Exemple :

In [11]:
exo3(g)
g.display()
Out[11]:
G G 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5

2. Algorithme de coloration de graphes¶

2.1 Algorithme Glouton Simple 🌶️¶

2.1.1 Exercice préliminaire¶

  • Contruire une fonction exo4(g,sommet,L) permettant de colorer le sommet sommet avec la couleur non blanche associée au plus petit entier qui n'est pas dans la liste L.
    On laissera les autres sommets en blancs.

Exemple :

In [13]:
exo4(g,2,[1,4,5,2])
### le sommet 2 devrait être colorer avec la couleur 3
### (3 est bien le plus petit entier qui n'est pas dans [1,4,5,2])
g.color
Out[13]:
[0, 0, 3, 0, 0, 0]

2.1.2 Ecriture de l'algorithme glouton simple¶

definition de glouton_simple(g)

S = liste des sommets de g

pour tout x de S
  pc = première couleur non utilisée par les voisins de x
  colorer le sommet x avec pc
fin pour tout

retourner g

  • Créer une fonction glouton_simple(g) permettant de colorer un graphe g grâce à l'algorithme glouton simplifié.

  • Tester glouton_simple(g).

Exemple :

In [15]:
glouton_simple(g)
g.display(title="G : glouton simple")
Out[15]:
G : glouton simple G : glouton simple 0 0 1 1 0--1 2 2 0--2 4 4 0--4 5 5 0--5 1--2 3 3 1--3 2--5
  • Construire le graphe $g_0$ ci-dessous, puis tester l'algorithme Glouton Simple.

Assurez vous de bien obtenir une coloration cohérente !

In [17]:
g0.display(title="G0")
Out[17]:
G0 G0 0 0 1 1 0--1 2 2 0--2 1--2 4 4 1--4 2--4 3 3 3--4
In [18]:
glouton_simple(g0)
g0.display(title="G0 : glouton simple")
Out[18]:
G0 : glouton simple G0 : glouton simple 0 0 1 1 0--1 2 2 0--2 1--2 4 4 1--4 2--4 3 3 3--4
  • Construire le graphe $g_1$ ci-dessous, puis tester l'algorithme Glouton Simple.

La coloration obtenue est-elle optimale ?

In [20]:
g1.display(title="G1 : glouton simple")
Out[20]:
G1 : glouton simple G1 : glouton simple 0 0 2 2 0--2 3 3 0--3 1 1 1--3 4 4 1--4 2--3 2--4 3--4
In [21]:
glouton_simple(g1)
g1.display(title="G1 : glouton simple")
Out[21]:
G1 : glouton simple G1 : glouton simple 0 0 2 2 0--2 3 3 0--3 1 1 1--3 4 4 1--4 2--3 2--4 3--4

2.2 Algorithme Glouton¶

2.2.1 Fonction lambda¶

Grâce au mot clef lambda, il est possible de créer à la volée des fonctions anonymes, c'est à dire des fonctions déclarées sans nom.

Sa syntaxe est : lambda arguments:expression

Les arguments peuvent être multiples, mais il n'y aura toujours qu'une seule expression

Exemples :

In [22]:
###Construisons une fonction qui calcule le carré d'un nombre
def carre(x):
    return x**2

###la même chose avec une fonction lambda
lambda x : x**2
Out[22]:
<function __main__.<lambda>(x)>
In [23]:
print(carre(3), (lambda x : x**2)(3))

9 9
In [24]:
###Construisons une fonction qui calcule la somme des carrés de deux nombres
def somme_carres(x,y):
    return x**2 + y**2

###la même chose avecune fonction lambda
lambda x,y : x**2 + y**2
Out[24]:
<function __main__.<lambda>(x, y)>
In [25]:
print(somme_carres(2,3), (lambda x,y : x**2 + y**2)(2,3))

13 13

2.2.2 Tri d'une liste¶

La fonction sorted() permet de trier une liste.

In [26]:
sorted([2,0,4,9,5])       #tri par ordre croissant, par défaut
Out[26]:
[0, 2, 4, 5, 9]
In [27]:
sorted([2,0,4,9,5],reverse=True)   #tri par ordre décroissant
Out[27]:
[9, 5, 4, 2, 0]
In [28]:
sorted(["AB","AAA","A","BA","B"])   #tri par ordre alphabétique
Out[28]:
['A', 'AAA', 'AB', 'B', 'BA']

La fonction sorted() admet un paramètre optionnel key.
Ce paramètre prend comme argument une fonction, qui va s'appliquer sur les valeurs de la liste à trier. Le tri se fait ensuite.

Exemples :

In [29]:
#Exemple 1
#tri suivant la longuer de la chaîne de caractère.
sorted(["AB","AAA","A","BA","B"], key=len)
Out[29]:
['A', 'B', 'AB', 'BA', 'AAA']
In [30]:
#Exemple 2
#définition de la fonction qui calcule le reste dans la division euclidienne modulo 3
def modulo3(n):
    return(n%3)
  
#tri suivant la valeur du reste modulo 3
sorted([2,0,4,9,5],key=modulo3)
Out[30]:
[0, 9, 4, 2, 5]
In [31]:
#Exemple 3
#même exemple que ci-dessus, mais avec l'utilisation d'une fonction lambda
  
sorted([2,0,4,9,5],key= (lambda n : n%3) )
Out[31]:
[0, 9, 4, 2, 5]
In [32]:
#Exemple 4
#tri suivant la distance de l'entier par rapport à 5
  
sorted([2,0,4,9,5],key= (lambda n : abs(n-5)) )
Out[32]:
[5, 4, 2, 9, 0]

2.2.3 Exercice¶

  • Construire une fonction tri_degre(g,Bool) qui renvoie la liste des sommets d'un graphe g triés suivant leur degré (dans l'ordre décroissant si Bool = True, croissant sinon).

Exemple :

In [34]:
tri_degre(g1,True)
Out[34]:
[3, 2, 4, 0, 1]

2.2.4 Ecriture de l'algorithme glouton¶

définition de glouton(g)

S = liste ordonnée des sommets, suivant la valeur décroissante de leur degré.

pour tout x de S
  pc = première couleur non utilisée par les voisins de x
  colorer le sommet x avec pc
fin pour tout

retourner g
  • Construire une fonction glouton(g) permettant de colorer un graphe g grâce à l'algorithme glouton.

Exemple :

In [36]:
glouton(g1)
g1.display(title="G1 : glouton")
Out[36]:
G1 : glouton G1 : glouton 0 0 2 2 0--2 3 3 0--3 1 1 1--3 4 4 1--4 2--3 2--4 3--4

3. Algorithme DSATUR¶

3.1 Ecriture de l'algorithme¶

On rappelle que : DSAT(x) = degré de saturation du sommet x = nombre de couleurs différentes dans les voisins de x

3.1.1 l'algorithme DSATUR en pseudo-langage :¶

défintion de DSATUR(g)

S = liste ordonnée des sommets, suivant la valeur décroissante de leur degré.
colorer un des sommets de degré max avec la plus petite couleur

tant que tous les sommets ne sont pas colorés
  choisir un sommet x non coloré avec un DSAT max (en cas d'égalité, choisir un sommet de degré max)
  pc = première couleur non encore utilisée par les voisins de x
  colorer le sommet x avec pc
fin tant que

retourner g

3.1.2 l'algorithme DSATUR en Python :¶

In [37]:
def dsatur(g):
    n = g.size()
    couleur = n*[0]
    
    #liste des sommets par ordre de degrés décroissants
    sommets_ord = tri_degre(g,True)
    
       
    #tant qu'il y a des sommets sans couleur    
    while 0 in couleur:
   
        #recherche du sommet à colorer, de degré de saturation maximum
        dsat = n*[0]
        degre_sat_max = 0
        sommetchoisi = sommets_ord[0]
        
        for i in sommets_ord:
            
            #si le sommet i est sans couleur
            if couleur[i]==0:

                vois = g.successors[i]
               
                #calcul du degré de saturation du sommet i
                couleurvois = []
                for k in vois:
                    if couleur[k]>0:
                        couleurvois = couleurvois+[couleur[k]]
                dsat[i] = len(np.unique(couleurvois))
                
                #le sommet i est-il de degre de saturation maximum ?
                if dsat[i]>degre_sat_max :
                    degre_sat_max = dsat[i]
                    sommetchoisi = i
        
        #couleur des voisins du sommet choisi
        vois_sommetchoisi = g.successors[sommetchoisi]
        couleurvois_sommetchoisi = []    
        for k in vois_sommetchoisi:
            couleurvois_sommetchoisi = couleurvois_sommetchoisi+[couleur[k]]        
        
        #choix de la plus petite couleur non présente chez les voisins du sommet choisi
        j=1
        while j in couleurvois_sommetchoisi:
            j=j+1
            
        #coloration du sommet choisi avec la couleur trouvée ci-dessus
        couleur[sommetchoisi]=j
        
        g.color = couleur
    return g

3.2 Exercice : comparaison des algorithmes.¶

  • Copier l'algorithme ci-dessus.

  • Construire le graphe $g2$ ci-dessous :

In [39]:
g2.display(title="G2")
Out[39]:
G2 G2 0 0 1 1 0--1 2 2 0--2 3 3 1--3 4 4 1--4 2--3 5 5 2--5 3--4 3--5 4--5

  • Trouver une coloration du graphe grâce à l'algorithme glouton simplifié.

  • Trouver une coloration du graphe grâce à l'algorithme glouton.

  • Trouver une coloration du graphe grâce à l'algorithme DSATUR.

In [40]:
glouton_simple(g2)
g2.display(title="G2 : glouton simple")
Out[40]:
G2 : glouton simple G2 : glouton simple 0 0 1 1 0--1 2 2 0--2 3 3 1--3 4 4 1--4 2--3 5 5 2--5 3--4 3--5 4--5
In [41]:
glouton(g2)
g2.display(title="G2 : glouton")
Out[41]:
G2 : glouton G2 : glouton 0 0 1 1 0--1 2 2 0--2 3 3 1--3 4 4 1--4 2--3 5 5 2--5 3--4 3--5 4--5
In [42]:
dsatur(g2)
g2.display(title="G2 : dsatur")
Out[42]:
G2 : dsatur G2 : dsatur 0 0 1 1 0--1 2 2 0--2 3 3 1--3 4 4 1--4 2--3 5 5 2--5 3--4 3--5 4--5

4. Applications¶

4.1 Théorème des 4 couleurs¶

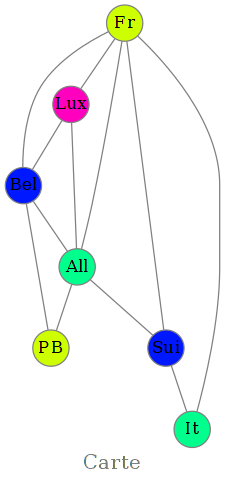
Un graphe est dit planaire ssi il existe une représentation de ce graphe où aucune arête n'en coupe une autre. Le théorème des 4 couleurs dit qu'un tel graphe peut être coloré avec au plus 4 couleurs.

  • Représenter par un graphe planaire les pays suivants : france, luxembourg, belgique, allemagne, pays-bas, suisse, italie (deux pays frontaliers seront reliés par une arête).

on pourra utiliser la liste des pays ["Fr","Lux","Bel","All","PB","Sui","It"], à rentrer dans le paramètre label de la méthode display.

  • Proposer une coloration, via un algorithme de votre choix.

Carte

4.2 Bonus : Mini Sudoku¶

4.2.1 Description du problème¶

On considère le mini-sudoku de 16 cases suivant :

grille

On cherche à remplir ce sudoku avec 4 couleurs en considérant les contraintes habituelles :

  • deux cases d'une même ligne ne peuvent pas avoir la même couleur

  • deux cases d'une même colonne ne peuvent pas avoir la même couleur

  • deux cases d'un même carré ne peuvent pas avoir la même couleur

4.2.2 Résolution¶

On donne ci-dessous le graphe sud à 16 sommets correspondant à une grille de mini-sudoku, sachant que deux sommets sont reliés ssi ils ne peuvent pas avoir la même couleur.

Exemple :
le sommet 0 est relié aux sommets 1, 2, 3, 4, 5, 8 et 12.
le sommet 10 est relié aux sommets 2, 6, 8, 9 ,11, 14 et 15.

In [44]:
sud = Graph(directed=False)
sud.successors = {0:{1,2,3,4,5,8,12}, 1:{0,2,3,4,5,9,13}, 2:{0,1,3,6,7,10,14}, 3:{0,1,2,6,7,11,15},
                  4:{0,1,5,6,7,8,12}, 5:{0,1,4,6,7,9,13}, 6:{2,3,4,5,7,10,14}, 7:{2,3,4,5,6,11,15},
                  8:{0,4,9,10,11,12,13}, 9:{1,5,8,10,11,12,13}, 10:{2,6,8,9,11,14,15}, 11:{3,7,8,9,10,14,15},
                  12:{0,4,8,9,13,14,15}, 13:{1,5,8,9,12,14,15}, 14:{2,6,10,11,12,13,15}, 15:{3,7,10,11,12,13,14}}
  • En modifiant l'algorithme DSATUR donné plus haut, construire une fonction sudoku(sommets, couleurs), qui propose une coloration du sudoku, en respectant les contraintes initiales suivantes :
    • sommets contient la liste de sommets initialement colorés
    • couleurs contient la liste des couleurs associées aux sommets précédents.

Exemple :

In [46]:
#dans l'exemple de l'illustration ci-dessus, les sommets déja colorés sont les sommets 0,2,4,11 et 13, associés aux couleurs 1,2,3,4 et 1

sudoku([0,2,4,11,13],[1,2,3,4,1]).display()
Out[46]:
G G 0 0 1 1 0--1 2 2 0--2 3 3 0--3 4 4 0--4 5 5 0--5 8 8 0--8 12 12 0--12 1--2 1--3 1--4 1--5 9 9 1--9 13 13 1--13 2--3 6 6 2--6 7 7 2--7 10 10 2--10 14 14 2--14 3--6 3--7 11 11 3--11 15 15 3--15 4--5 4--6 4--7 4--8 4--12 5--6 5--7 5--9 5--13 6--7 6--10 6--14 7--11 7--15 8--9 8--10 8--11 8--12 8--13 9--10 9--11 9--12 9--13 10--11 10--14 10--15 11--14 11--15 12--13 12--14 12--15 13--14 13--15 14--15

4.2.3 Représentation¶

  • Construire une fonction sudoku_tableau(sommets, couleurs) qui propose une représentation du sudoku sous forme de tableau 4 par 4.

Exemple :

In [48]:
#Affichage du sudoku résolu

sudoku_tableau([0,2,4,11,13],[1,2,3,4,1])
Out[48]:
array([[1., 4., 2., 3.],
       [3., 2., 4., 1.],
       [2., 3., 1., 4.],
       [4., 1., 3., 2.]])

5. Mega Bonus 🌶️🌶️¶

  • Construisez votre propre fonction permettant de colorer un graphe via l'algorithme DSATUR.