Problèmes classiques de la théorie des graphes¶

In [1]:
import numpy as np
from graph import *

En plus des packages habituels, nous aurons besoin du package math, pour sa représentation de l'infini

In [2]:
from math import inf

inf vérifie les propriétés classiques :

In [3]:
print(inf > 9999)
print(inf + 82 == inf)
print(inf + 1 > inf)
print(inf*(-72) == -inf)

True
True
False
True

1. Graphes valués¶

1.1 Matrice de poids¶

Un graphe valué est un graphe auquel on ajoute un poids, positif ou nul, sur ses arcs/arêtes.

Un graphe valué peut être représenté par sa matrice de poids M définie de la façon suivante :

$M_{i,j}=+\infty$ si il n'y pas d'arcs/arêtes reliant i à j
$M_{i,j}=$ valuation de l'arc/arête (i, j)

Exemple : le graphe orienté valué $GV1$ a pour matrice de poids $MV1$.

In [4]:
MV1 = np.array([ [inf,2,4,inf,inf],
                 [inf,inf,7,inf,inf],
                 [inf,9,inf,7,5],
                 [inf,inf,inf,inf,inf],
                 [8,inf,inf,inf,inf] ])

Un graphe valué sera créé grâce à l'attribut weight, à qui sera affectée la matrice de poids (cet attribut a pour valeur par défaut une liste vide).

In [5]:
gv1 = Graph(weight=MV1)
gv1.successors = {0:{1,2},
                  1:{2},
                  2:{1,3,4},
                  3:set(),
                  4:{0}}
gv1.display(title="GV1")
Out[5]:
GV1 GV1 0 0 1 1 0->1 2.0 2 2 0->2 4.0 1->2 7.0 2->1 9.0 3 3 2->3 7.0 4 4 2->4 5.0 4->0 8.0
In [6]:
# on peut accéder la matrice de poids via l'attribut weight
gv1.weight
Out[6]:
array([[inf,  2.,  4., inf, inf],
       [inf, inf,  7., inf, inf],
       [inf,  9., inf,  7.,  5.],
       [inf, inf, inf, inf, inf],
       [ 8., inf, inf, inf, inf]])
In [7]:
# on peut aussi modifier un poids existant via l'attribut weight.
gv1.weight[0,1] = 10
print(gv1.weight)
gv1.display(title="GV1")

[[inf 10.  4. inf inf]
 [inf inf  7. inf inf]
 [inf  9. inf  7.  5.]
 [inf inf inf inf inf]
 [ 8. inf inf inf inf]]
Out[7]:
GV1 GV1 0 0 1 1 0->1 10.0 2 2 0->2 4.0 1->2 7.0 2->1 9.0 3 3 2->3 7.0 4 4 2->4 5.0 4->0 8.0

Attention :
Changer un inf en un nombre réel dans la matrice ne va pas ajouter automatiquement l'arc valué correspondant. Il faudra penser à modifier le dictionnaire contenant les successeurs !

1.2 Construction d'un graphe valué¶

  • Construire une fonction matricepoids_vers_graphe(M) qui construit directement le graphe orienté valué de matrice de poids $M$.

Exemple :

In [8]:
# on donne la matrice MV2 suivante :
MV2 = np.array([ [inf,8,2,inf,inf],
                 [inf,inf,inf,1,inf],
                 [inf,5,inf,11,1],
                 [inf,inf,inf,inf,inf],
                 [inf,inf,inf,9,inf]])
In [10]:
gv2 = matricepoids_vers_graphe(MV2)
print(gv2.successors)
gv2.display(title = "GV2")

{0: {1, 2}, 1: {3}, 2: {1, 3, 4}, 3: set(), 4: {3}}
Out[10]:
GV2 GV2 0 0 1 1 0->1 8.0 2 2 0->2 2.0 3 3 1->3 1.0 2->1 5.0 2->3 11.0 4 4 2->4 1.0 4->3 9.0

2. Problème du plus court chemin¶

Dans cette partie, les graphes seront orientés, à valuations positives.

2.1 Algorithme de Bellman¶

définition de bellman(g)

M = matrice de poids de g
Dist = liste des distances depuis le sommet 0, dont chaque élément est initialisé à l'infini
Dist[0] = 0

tant que Dist change

  pour tout sommet i
    pour tout sommet j
      si Dist[i] + M[i,j] < Dist[j]
      alors Dist[j] = Dist[i] + M[i,j]
      fin si
    fin pour
  fin pour

fin tant que

retourner Dist

  • Construire une fonction bellman(g), qui renvoie les distances du plus court chemin du sommet $0$ à tous les autres, dans un graphe orienté valué g, à l'aide de l'algorithme de Bellman.

  • Tester bellman avec le graphe gv2.

In [12]:
bellman(gv2)
Out[12]:
[0, 7.0, 2.0, 8.0, 3.0]

2.2 Exercice : algorithme de Dijkstra 🌶️¶

définition de dijkstra(g)

M = matrice de poids de g
Dist = liste des distances depuis le sommet 0, dont chaque élément est initialisé à l'infini
Dist[0] = 0

tant que il y a des sommets non marqués

  choisir un sommet i non marqué, tel que Dist[i] soit minimale
  marquer i

  pour tout sommet j non marqué
    si Dist[i] + M[i,j] < Dist[j]
    alors Dist[j] = Dist[i] + M[i,j]
    fin si
  fin pour

tant que

retourner Dist
  • Reprendre l'exercice précedent, avec une fonction dij(g) et l'algorithme de Dijkstra.

Rq : on pourra par exemple créer une liste marquage, avec marquage[i]=True si le sommet i est marqué, False sinon.

Exemple :

In [14]:
dij(gv2)
Out[14]:
[0, 7.0, 2.0, 8.0, 3.0]

2.3 Application : ordonnancement¶

algorithme du plus long chemin¶

On veut maintenant créer un algorithme du plus long chemin. On supposera donc que le graphe n'a pas de circuits, afin de ne pas boucler à l'infini.

  • Que doit-on modifier dans l'algorithme de Bellman pour traiter un problème de plus long chemin ?

  • Créer une fonction bellmanlong(g) qui renvoie les distances du plus long chemin du sommet 0 à tous les autres.

Exemple :

In [16]:
bellman_long(gv2)
Out[16]:
[0, 8.0, 2.0, 13.0, 3.0]

un problème d'ordonnancement¶

Soit le problème d'ordonnancement suivant :

tâches contraintes durée (jours)
(0) début du projet 0
(1) aucune contrainte 3
(2) commence au plus tôt après la fin de (3), et 9 jours après la fin de (1) 6
(3) commence au plus tôt 5 jours après le début du projet, et 4 jours après la fin de (1) 4
(4) fin du projet 0

On associe à ce problème d'ordonnancement un graphe potentiel-tâche :
les sommets sont les tâches, et un arc (i,j) a une valuation k ssi la tâche j commence au plus tôt k jours après le début de la tâche i.

  • Tracer le graphe gA potentiel-tâche du projet ci-dessus.
In [18]:
gA.display(title="potentiel_tache")
Out[18]:
potentiel_tache potentiel_tache 0 0 1 1 0->1 0.0 3 3 0->3 5.0 2 2 1->2 12.0 1->3 7.0 4 4 2->4 6.0 3->2 4.0

L'objectif est de trouver les dates de début au plus tôt de chaque tâche, pour terminer le projet le plus rapidement possible. Il suffit alors de calculer les chemins les plus long depuis le sommet 0 à tous les autres.

  • Trouver les dates de début au plus tôt de chacune des tâches.
Out[14]:
[0, 0.0, 12.0, 7.0, 18.0]

3. Bonus : algorithme de Prim 🌶️🌶️¶

3.1 Enoncé du problème¶

Les villes Zérocity, Unville, Deuxbourg, Trois-sur-marne et Saint-Quatre souhaitent être reliées par un réseau de trains. Pour cela, une étude a été menée sur le coût de projet, aboutissant au graphe reseau suivant :

In [22]:
reseau.display(title="réseau de trains")
Out[22]:
réseau de trains réseau de trains 0 0 1 1 0--1 2.0 2 2 0--2 4.0 3 3 0--3 3.0 4 4 0--4 6.0 1--2 7.0 2--3 2.0 2--4 8.0 3--4 1.0

Par exemple, cela couterait 3 millions de relier directement Zérocity à Trois-sur-marne, et 6 millions de relier directement Zérocity à Saint-Quatre.

Le regroupement de communes décide d'autoriser les changements de lignes, et de ne construire que les lignes nécessaires, afin d'assurer un coût total minimal.

Mathématiquement, il s'agit de construire un arbre couvrant de poids minimal, c'est à dire un arbre passant par tous les sommets du graphe, dont la somme des poids des arêtes est minimale. L'algorithme proposé pour résoudre le problème est l'algorithme de Prim.

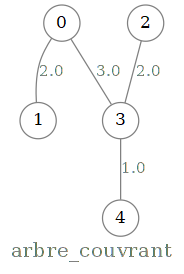
Dans l'exemple, l'arbre couvrant serait :

arbre_couvrant

définition de prim(g)

marquer le sommet 0
arbre = arbre résultat, ne contenant initialement pas d'arêtes.

tant qu' il reste des sommets non marqués
  {x, y} = arête de poids minimal, joignant un sommet marqué x à un sommet non marqué y
  marquer y
  ajouter l'arête {x,y} à l'arbre 
fin tant que

retourner arbre

3.2 Algorithme de Prim¶

  • Construire la matrice de poids conrespondant au graphe ci-dessus.

Attention, le graphe étant non orienté, il faut que la matrice de poids soit symétrique !

  • Construire une fonction prim(g) qui retourne l'arbre couvrant de poids minimum d'un graphe valué non orienté g.
    Tracer cet arbre.
In [23]:
arbre_couvrant = prim(reseau)
arbre_couvrant.display(title="arbre couvrant")
Out[23]:
arbre couvrant arbre couvrant 0 0 1 1 0--1 2.0 3 3 0--3 3.0 2 2 2--3 2.0 4 4 3--4 1.0
In [24]:
arbre_couvrant.successors
Out[24]:
{0: {1, 3}, 1: {0}, 2: {3}, 3: {0, 2, 4}, 4: {3}}
In [25]:
arbre_couvrant.weight
Out[25]:
array([[inf,  2., inf,  3., inf],
       [ 2., inf, inf, inf, inf],
       [inf, inf, inf,  2., inf],
       [ 3., inf,  2., inf,  1.],
       [inf, inf, inf,  1., inf]])