Exemple de labyrinthe parfait :
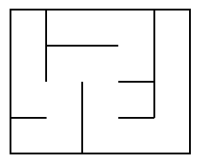
Exemple de labyrinthe imparfait :

Références :
Wikipedia pour l'algorithme d'exploration exhaustive
"Mazes for Programmers" de Jamis Buck, qui traite de différents problèmes liés aux labyrinthes, et propose des implémentations en Ruby.
L'objectif de cette SAE est de voir différents algorithmes permettant de construire des labyrinthes, puis de les résoudre.
Nous nous restreindrons à des labyrinthes dits parfaits, c'est à dire des labyrinthes où chaque cellule peut joindre une autre par un chemin unique.
A l'inverse, les labyrinthes pouvant contenir des ilôts, des boucles ou des cellules inaccessibles sont dits imparfaits, et ne seront pas étudiés dans ce projet.
Exemple de labyrinthe parfait :

Exemple de labyrinthe imparfait :

Remarque :Un labyrinthe parfait peut être vu comme un arbre, où chaque sommet est une cellule (= une "case") du labyrinthe.
Le labyrinthe parfait ci-dessus donne l'arbre :
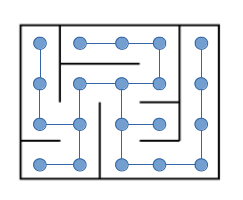
Il y a donc un lien très fort entre labyrinthe parfait et théorie des arbres, et nous allons voir que les algorithmes utilisés dans cette SAE sont proches de ceux vus en TP de graphes.
Avant de construire un labyrinthe, nous allons commencer par construire une grille.
Nous avons pour cela défini plusieurs classes :
la classe UneCellule, permettant de créer une cellule de la grille. Cette cellule sera caractérisée par sa position dans la grille, et possède 4 "bords" appelés murs : le mur Nord, le mur Sud, le mur Est et le mur Ouest.
la classe Grille, qui est un tableau de nl lignes et nccolonnes de cellules.
########
class UneCellule:
"""
définition d'une cellule
"""
def __init__(self,x, y):
"""
créer une cellule positionnée en (x=ligne, y=colonne)
"""
self.x = x
self.y = y
#les murs sont dans l'ordre : N, S, E, O.
#la valeur est à True si un mur est présent, False sinon
self.murs = {'N': True, 'S': True, 'E': True, 'O': True}
########
class Grille :
"""
construction d'une grille de cellules
"""
def __init__(self, nl, nc):
"""
construction d'une grille de dimension (nl, nc)
"""
self.nl = nl
self.nc = nc
self.cadrillage = []
for i in range(nl):
GrilleLigne=[]
for j in range(nc):
GrilleLigne.append(UneCellule(i,j))
self.cadrillage.append(GrilleLigne)
def cellule(self, x, y):
"""
retourne la cellule de la grille de position (x=ligne, y=colonne)
"""
return self.cadrillage[x][y]
def __str__(self):
"""
retourne une chaine de caractères représentant le labyrinthe
pour les cellules touchant le bord gauche ou le bord du haut de la grille, les 4 murs sont représentés.
pour les autres, seuls les murs Est et Sud sont représentés
"""
laby_lignes = []
laby_l = ['+']
for y in range(self.nc):
if self.cadrillage[0][y].murs['N']:
laby_l.append('---+')
else :
laby_l.append(' +')
laby_lignes.append(''.join(laby_l))
for x in range(0,self.nl):
if self.cadrillage[x][0].murs['O'] :
laby_l = ['|']
else :
laby_l = [' ']
for y in range(self.nc):
if self.cadrillage[x][y].murs['E']:
laby_l.append(' |')
else:
laby_l.append(' ')
laby_lignes.append(''.join(laby_l))
laby_l = ['+']
for y in range(self.nc):
if self.cadrillage[x][y].murs['S']:
laby_l.append('---+')
else:
laby_l.append(' +')
laby_lignes.append(''.join(laby_l))
#laby_lignes.append('\n')
return '\n'.join(laby_lignes)
Afin de mieux comprendre les classes ci-dessus, voyons quelques exemples.
# Contruction d'une grille de 4 lignes par 6 colonnes
grilleTest = Grille(4,6)
print(grilleTest)
+---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
# Accès aux dimensions de la grille
print(grilleTest.nl, grilleTest.nc)
4 6
# Accès à une cellule de la grille
cell =grilleTest.cellule(2,3)
# Accès à la position d'une cellule (sous forme (ligne, colonne))
print(cell.x, cell.y)
2 3
# Accès aux murs d'une cellule
cell.murs
{'N': True, 'S': True, 'E': True, 'O': True}
# Accès au mur Est d'une cellule
cell.murs['E']
True
Reprenons la grille grilleTest précédente, et commençons par détruire quelques murs.
# Détruisons le mur Est de la cellule 'cell' positionnée en (2,3)
cell.murs['E']=False
print(grilleTest)
+---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
On remarque que le mur Est de la cellule (2,3) est bien détruit. Mais pour autant ... le mur Ouest de la cellule (2,4) est encore intact !!
grilleTest.cellule(2,4).murs['O']
True
Pourtant, en terme de représentation du labyrinthe, le mur Est de (2,3) est bien le même mur que le mur Ouest de (2,4)!
Plus problèmatique, encore : reconstruisons le mur Est de (2,3), détruisons le mur Ouest de (2,4), et visualisons le résultat :
grilleTest.cellule(2,3).murs['E']=True
grilleTest.cellule(2,4).murs['O']=False
print(grilleTest)
+---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
Le mur Ouest de (2,4) est bien détruit, et pourtant cela n'apparaît pas dans la visualisation de la grille.
Cela est du à la façon de construire la représentation de la grille. Par commodité, seuls les murs Est et Sud d'une cellule sont traçés. Cela permet de ne pas afficher de 'doubles murs', mais en contrepartie le lien qui existe entre deux cellules de part et d'autres d'un même mur est perdu.
Nous aurons le même problème avec par exemple le mur Nord de (2,3) et le mur Sud de (1,3).
# casser le mur Nord de (2,3) passera inaperçu
grilleTest = Grille(4,6)
grilleTest.cellule(2,3).murs['N']=False
print(grilleTest)
+---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
# si on veut voir disparaitre le mur, il faut détruire le mur Sud de (1,3)
grilleTest.cellule(1,3).murs['S']=False
print(grilleTest)
+---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+ +---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
Exception : pour les cellules touchant le bord gauche de la grille, ou le bord du haut, les 4 murs sont bien représentés, pas seulement les murs Est et Sud.
Afin de palier au problème évoqué plus haut, créer une fonction effaceMur(grille, coord, orientation) qui pour une grille grille :
orientation (c-à-d 'N', 'S', 'E' ou 'O') de la cellule de position coord.Remarque
On fera attention aux cellules situées au bord de la grille, qui n'auront pas forcément de cellules voisines.
Exemple :
grilleTest = Grille(4,6)
# on efface le mur Ouest de la cellule (3,2)
effaceMur(grilleTest,(3,2),'O')
# affichage de la cellule modifiée
print('(3,2) :',grilleTest.cellule(3,2).murs)
# affichage de la cellule 'voisine', ici la cellule (3,1)
print('(3,1) :',grilleTest.cellule(3,1).murs)
# affichage de la grille
print(grilleTest)
(3,2) : {'N': True, 'S': True, 'E': True, 'O': False}
(3,1) : {'N': True, 'S': True, 'E': False, 'O': True}
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | |
+---+---+---+---+---+---+
grilleTest = Grille(4,6)
# on efface le mur Nord de la cellule (2,1)
effaceMur(grilleTest,(2,1),'N')
# affichage de la cellule modifiée
print('(2,1) :',grilleTest.cellule(2,1).murs)
# affichage de la cellule 'voisine', ici la cellule (1,1)
print('(1,1) :',grilleTest.cellule(1,1).murs)
# affichage de la grille
print(grilleTest)
(2,1) : {'N': False, 'S': True, 'E': True, 'O': True}
(1,1) : {'N': True, 'S': False, 'E': True, 'O': True}
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+ +---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
grilleTest = Grille(4,6)
# on efface le mur Est de la cellule (0,5)
effaceMur(grilleTest,(0,5),'E')
# affichage de la cellule modifiée
print('(0,5) :',grilleTest.cellule(0,5).murs)
# Attention : cette cellule n'a pas de cellule voisine située à sa droite, donc il ne doit pas y avoir de modifications supplémentaires !
# affichage de la grille
print(grilleTest)
(0,5) : {'N': True, 'S': True, 'E': False, 'O': True}
+---+---+---+---+---+---+
| | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
| | | | | | |
+---+---+---+---+---+---+
Nous allons voir dans cette partie plusieurs algorithmes permettant de créer des labyrinthes parfaits. Nous ne nous occuperons pas de placer les entrées et sorties du labyrinthes, qui n'influent pas sur la construction.
Ainsi, les murs extérieurs de la grille ne seront jamais détruits.
Nous allons construire notre premier labyrinthe, à l'aide d'un algorithme très simple. En voici sa description :
effaceMur).Construire une fonction arbreBinaire(grille) qui retourne un labyrinthe créé par l'algorithme précédent.
Exemple :
ab = Grille(4,6)
print(arbreBinaire(ab))
+---+---+---+---+---+---+ | | | | | | + +---+ + + + + | | | | | | + + + +---+ + + | | | | | | | + + + + + + + | | +---+---+---+---+---+---+
Essayez de construire plusieurs labyrinthes à l'aide de cette méthode. Qu'ont en commun tous ces labyrinthes ?
Cet algorithme simple est très similaire à l'algorithme précédent. Le labyrinthe est généré une ligne à la fois : pour chaque cellule de cette ligne, on décide aléatoirement s'il faut détruire le mur Est ou pas.
Exemple :
Commençons par la ligne du haut.
Imaginons que le sort décide de ne pas détruire le mur Est de (0,0). On choisit donc aléatoirement parmi les cellules du passage et on détruit le mur Sud de la cellule choisie. Comme pour l'instant il n'y a que (0,0) dans le passage, on détruit son mur Sud.
Imaginons maintenant que le sort ait décidé qu'aux étapes 2 et 3, les murs Est de (0,1) et de (0,2) soient détruits.
On se retrouve alors dans cette situation à la fin de l'étape 3 :
print(etape3)
+---+---+---+---+---+---+ | | | | | + +---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
A l'étape 4, le sort décide de ne pas détruire le mur Est de (0,3). Ce passage horizontal est terminé. On choisit aléaoirement parmi les cellules du passage, à savoir (0,1), (0,2) et (0,3) laquelle vera son mur Sud détruit.
Remarque : la cellule (0,0) ne fait pas partie du même passage horizontal !
Imaginons que c'est la cellule (0,2) qui perd son mur Sud. On se retrouve ainsi à la fin de l'étape 4 :
print(etape4)
+---+---+---+---+---+---+ | | | | | + +---+ +---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
On commence donc un nouveau passage horizontal à l'étape 5, et le traitement de la cellule (0,4). Imaginons que son mur Est soit détruit.
On traite alors à l'étape 6 la cellule (0,5), et comme elle est en bout de grille son mur Est ne peut pas être détruit. On choisit donc un mur Sud à abattre, parmi les cellules du passage horizontal actuel, à savoir (0,4) et (0,5) ... Le hasard décidant de détruire le mur Sud de (0,4), voici la situation à la fin du traitement de la première ligne :
print(etape6)
+---+---+---+---+---+---+ | | | | + +---+ +---+ +---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+ | | | | | | | +---+---+---+---+---+---+
Et ainsi de suite, on traite une par une chaque ligne. A savoir que pour les cellules de la dernière ligne, on détruira forcément les murs Est (histoire de ne pas sortir de la grille), et on ne détruira aucun mur de la dernière cellule située en bas à droite.
Construire une fonction sidewinder(grille) qui réalise l'algorithme précédent.
Exemple :
SW = Grille(4,6)
print(sidewinder(SW))
+---+---+---+---+---+---+ | | | +---+ +---+ +---+---+ | | | + +---+---+---+---+ + | | | | + +---+---+ +---+ + | | +---+---+---+---+---+---+
Essayez de construire plusieurs labyrinthes à l'aide de cette méthode. Qu'ont en commun tous ces labyrinthes ?
Cet algorithme s'apparente au parcours en profondeur d'arbre vu en cours. Voici la description de cet algorithme sur wikipedia:
L'utilisation de la récursivité n'étant pas au programme, nous allons comme en TP de graphes utiliser une Pile.
Voila la description de l'algorithme :
definition de explorationE(grille) Visite = tableau 2D (ou matrice ...) de même taille que la grille. Ce tableau nous servira à savoir si une cellule a déja été traitée ou non Pile = une liste, vide pour l'instant On choisit aléatoirement une cellule, sous forme d'un couple (ligne, colonne) On la met dans Pile, et on indique dans le tableau Visite que cette cellule a été traitée. tant que Pile non vide soit (i,j) le premier élément de Pile on recherche les voisins non encore traités de (i,j) si il y en a soit (k,l) = un de ces voisins, choisi au hasard on détruit le mur entre (k,l) et la cellule (i,j) on indique dans Visite que (k,l) a été traitée on ajoute (k,l) au début de Pile sinon on retire le premier élément de Pile retourner grille
Construire une fonction explorationE(grille) qui réalise l'algorithme précédent.
Exemple :
grilleTest = Grille(4,6)
exp = explorationE(grilleTest)
print(exp)
+---+---+---+---+---+---+ | | | +---+ +---+ + +---+ | | | | + +---+ +---+---+ + | | | | | + + + + +---+ + | | | | +---+---+---+---+---+---+
L'article wikipedia propose une autre façon de créer un labyrinthe parfait :
La fusion aléatoire des chemins
Proposer une fonction fusion(grille) qui construit un labyrinthe parfait sur ce principe.
Nous allons proposer maintenant une résolution de labyrinthe, reposant sur un parcours en largeur du labyrinthe.
Pour cela, nous ferons la convention que l'entrée du labyrinthe est la cellule en haut à gauche et que la sortie est la cellule située en bas à droite.
laby = explorationE(Grille(5,7))
effaceMur(laby,(0,0),'O')
effaceMur(laby,(4,6),'E')
print(laby)
+---+---+---+---+---+---+---+
|
+ +---+ +---+---+---+ +
| | | |
+---+---+---+ +---+ +---+
| | | |
+ +---+ +---+---+---+ +
| | | | |
+ + +---+ +---+---+ +
| |
+---+---+---+---+---+---+---+
Nous dirons que deux cellules sont attenantes ssi il n'y a pas de murs entre elles.
Construire une fonction attenantes(labyrinthe,coord) qui retourne les cellules attenantes à la cellule de position coord.
Exemple :
print(attenantes(laby,(1,3)))
[(2, 3), (1, 4), (1, 2)]
print(attenantes(laby,(1,1)))
[(1, 0)]
L'objectif de cette partie est d'obtenir un tableau (ou une matrice ...) notée D, où :
D[i,j] = nombre de cases nécéssaires pour se rendre de la case (0,0) à la case (i,j).
Par exemple, voici la matrice D correspondant au labyrinthe laby précédent :
print(laby)
print(distance(laby))
+---+---+---+---+---+---+---+
|
+ +---+ +---+---+---+ +
| | | |
+---+---+---+ +---+ +---+
| | | |
+ +---+ +---+---+---+ +
| | | | |
+ + +---+ +---+---+ +
| |
+---+---+---+---+---+---+---+
[[ 0. 1. 2. 3. 4. 5. 6.]
[ 1. 2. 3. 4. 5. 6. 7.]
[18. 19. 20. 5. 6. 7. 8.]
[17. 16. 21. 12. 11. 10. 9.]
[16. 15. 14. 13. 12. 11. 10.]]
Nous allons cette fois utiliser une File. Voici la description de l'algorithme :
definition de distance(labyrinthe) D = tableau 2D (ou matrice ...) de même taille que la grille. Ce tableau contiendra les distances depuis (0,0), et peut être initialisé à l'infini File = une liste, vide pour l'instant Initialisation : D[0,0] = 0 On met (0,0) dans File tant que File non vide soit (i,j) le premier élément de File on recherche les cellules attenantes à (i,j) non encore traitées on met ces cellules à la fin de File ces cellules reçoivent dans D la valeur D[i,j]+1 on retire le premier élément de File retourner D
Construire une fonction distance(labyrinthe) qui retourne la matrice D pour un labyrinthe donné.
Pour trouver la solution au labyrinthe, il "suffit" de partir de la cellule en bas à droite, et de remonter le chemin dans D en suivant l'ordre décroissant.
Construire une fonction resolution(labyrinthe) qui retourne le chemin permettant de résoudre le labyrinthe.
Exemple :
print(laby,'\n')
print(resolution(laby))
+---+---+---+---+---+---+---+
|
+ +---+ +---+---+---+ +
| | | |
+---+---+---+ +---+ +---+
| | | |
+ +---+ +---+---+---+ +
| | | | |
+ + +---+ +---+---+ +
| |
+---+---+---+---+---+---+---+
[(0, 0), (0, 1), (0, 2), (1, 2), (1, 3), (1, 4), (1, 5), (2, 5), (2, 6), (3, 6), (4, 6)]
La résolution précédente repose sur le fait que l'on connaisse la structure globale du labyrinthe.
Prenons désormais un point de vue local : une personne est placée à l'entrée du labyrinthe, et ne sait rien de sa structure. Elle est incapable de faire la différence entre deux positions dans le labyrinthe.
Un moyen bien connu pour trouver la sortie est la méthode de la main droite, qui consiste à longer systématiquement le mur de droite, sans le lacher.
Efficace, cette méthode peut néanmoins aboutir à explorer une grande partie du labyrinthe, et même la totalité dans le pire des cas.
Construire une fonction parcoursMD(labyrinthe), qui retourne le chemin emprunté pour sortir du labyrinthe en utilisant la méthode de la main droite.
Remarque : La personne dans le labyrinthe reconnaît la sortie quand elle l'atteint. Pour simuler ceci et simplifier un peu le problème, nous pouvons considérer qu'il est connu que le départ est en haut à gauche et la sortie en bas à droite. La taille de la grille est aussi connue.
Exemple :
print(laby,'\n')
print(parcoursMD(laby))
+---+---+---+---+---+---+---+
|
+ +---+ +---+---+---+ +
| | | |
+---+---+---+ +---+ +---+
| | | |
+ +---+ +---+---+---+ +
| | | | |
+ + +---+ +---+---+ +
| |
+---+---+---+---+---+---+---+
[(0, 0), (1, 0), (1, 1), (1, 0), (0, 0), (0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (2, 4), (2, 3), (1, 3), (1, 4), (1, 5), (2, 5), (2, 6), (3, 6), (3, 5), (3, 4), (3, 3), (4, 3), (4, 2), (4, 1), (3, 1), (4, 1), (4, 0), (3, 0), (2, 0), (2, 1), (2, 2), (3, 2), (2, 2), (2, 1), (2, 0), (3, 0), (4, 0), (4, 1), (4, 2), (4, 3), (3, 3), (3, 4), (3, 5), (3, 6), (4, 6)]