Description univariée
Module de première année de BUT informatique, Reims. TP de statistiques descriptives.
Les statistiques descriptives sont un ensemble d’outils permettant de synthétiser, résumer, visualiser les données. L’objectif est de comprendre ces données.
Une donnée est une valeur issue du codage de l’observation d’une caractéristique sur un objet donné.
On appelle :
Exemple : on observe la couleur des cheveux, le poids et la taille d’un groupe d’individus ; l’observation de ces trois caractères sur les individus définissent 3 variables sur la population constituée de ces personnes.
Les observations doivent être codées avant d’être considérées comme des données. Il existe alors deux possibilités :
Au delà de la représentation informatique des observations (nous en reparlerons), on distingue plusieurs type de données associés à ces observations. Cette typologie permet de catégoriser les variables.
En bref LES VARIABLES
Si effectuer des opérations sur les valeurs n’a pas de sens, on a vraissemblablement affaire à une variable qualitative. Si les modalités semble avoir un ordre naturel, il s’agit certainement d’une variable qualitative ordinale. Sinon, c’est une qualitative nominale. Si on peut réaliser des opérations sur les valeurs (exemple de question à se poser : « est-ce que l’écart entre deux valeurs signifie quelque chose ?»), la variable est quantitative. Si on peut lister l’ensemble des valeurs possibles facilement, c’est sans doute une quantitative discrète sinon, c’est plus probablement une quantitative continue.
Exercice TYPES DE VARIABLES
On a relevé, dans un groupe d’étudiants, les caractéristiques suivantes :
51100, 08200, 51120, 02150, ...184,164,178,192, ...G, T, G, G, ...12.75, 10.5, 8.333, 15.125, ...1, 5, 3, 1, ...Déterminer le type de chaque variables.
La façon dont on représente et encode informatiquement les valeurs est variable. On peut aussi transformer les données d’un type de variable à un autre. Ainsi, il arrive fréquemment qu’on représente les modalités d’une variable qualitative à l’aide d’entiers, ou encore qu’on transforme une variable quantitative en variable discrète ou en qualitative ordinale.
Exercice MODIFICATION D’UNE SÉRIE
Dans cet exercice, nous allons écrire des petites fonctions de transformation des données.
Écrire :
where_none(dat:list) qui localise
d’éventuelles valeurs manquantes (que nous encoderons avec
None) et retourne la liste des indices correspondants.remove_data(dat:list, pos:list) qui
retourne une copie de dat, dont on a supprimé les éléments
situés aux positions fournies dans la liste pos.replace_value(dat:list, value:list, repvalue:list) qui
remplace, dans une copie de ldat, les valeurs contenues
dans value par celles contenues dans repvalue
(par exemple, toutes les value[2] doivent être remplacées
par repvalue[2])Remarque importante : les fonctions à écrire dans cet exercice et dans les suivants ne doivent pas modifier les données passées en argument ; elles doivent retourner des données issues de ces éventuelles transformations.
Exemples de comportements attendus de ces fonctions :
data1 = [11,5,6,7,5,2,3,6,None,1,2,5,4,9,6,3,5,8,None]
data2 = ["toto","toto","tata","toto","titi","toto","tata","tata"]
data3 = [None, "None"]
print(where_none(data1))[8, 18]print(where_none(data2))[]print(where_none(data3))[0]print(remove_data(data1,where_none(data1)))[11, 5, 6, 7, 5, 2, 3, 6, 1, 2, 5, 4, 9, 6, 3, 5, 8]print(data1)
replace_value(data1,[8,11,None],[-8,-11,0])[11, 5, 6, 7, 5, 2, 3, 6, None, 1, 2, 5, 4, 9, 6, 3, 5, 8, None]
[-11, 5, 6, 7, 5, 2, 3, 6, 0, 1, 2, 5, 4, 9, 6, 3, 5, -8, 0]Nous allons maintenant écrire une autre fonction très utile permettant de discrétiser une variable quantitative continue.
Exercice DISCRÉTISATION
Écrire une fonction cut(dat, split) qui transforme une
variable continue dat en remplaçant chaque valeur par
l’intervalle -défini par les bornes contenues dans split-
auquel cette valeur appartient. Si split est une liste de
\(p+1\) valeurs \(s_0, s_1, \ldots, s_{p}\), l’espace des
valeurs sera découpé en \(p\)
intervalles contigüs \([s_0,s_1], ]s_2,s_3],
\ldots, ]s_{p-1},s_p]\).
Les intervalles seront représentés par des chaînes de caractères.
Exemples :
# Générons des données aléatoires (des float arrondis à 10^-2 entre 0 et 20)
import random
data = [round(random.random()*20,2) for _ in range(10)]
print(data)[0.64, 9.75, 19.34, 3.92, 13.69, 18.81, 0.54, 18.76, 3.09, 13.88]# Discrétisation
cut(dat=data, split=[0,5,10,15,20])['(0,5]',
'(5,10]',
'(15,20]',
'(0,5]',
'(10,15]',
'(15,20]',
'(0,5]',
'(15,20]',
'(0,5]',
'(10,15]']Étudier une variable d’un jeu de données, indépendamment des autres, relève des statistiques descriptives univariées, et consiste à tenter de résumer, observer et décrire les principales caractéristiques de la série des valeurs qui la constituent, dès lors qu’elles sont assez nombreuses (on parle de série statistique).
On dispose pour ça de différents outils :
Globalement, tous ces outils reviennent à décrire la distribution de la série :
La distribution statistique groupée, est une
représentation de la distribution d’une variables qualitative ou d’une
variable quantitative qu’on aurait découpée en classe (voir plus haut
cut). Elle représente une série statistique à l’aide des
classes et du nombre de valeurs (effectif) ou de la
proportion de valeur (fréquence) dans chacune de ces
classes. On peut ensuite déterminer le mode de la série
correspondant à la classe de plus grand effectif.
Exercice DISTRIBUTION GROUPÉE
Écrire une fonction get_gdistr(dat) qui retourne un dictionnaire dont
les clés sont les modalités, et les valeurs sont des tuples constitués
de l’effectif et de la fréquence de chaque modalité (effectif = nombre
de fois où apparaît la modalité dans dat ; fréquence =
effectif de la modalité / nombre de données dans dat).
Exemple :
# Données de test
data = ["toto","toto","tata","toto","titi",
"toto","tata","tata","toto","toto",
"toto","toto","titi","toto","titi",
"tata","toto","tata","tata","toto"]# Construction de la ditribution groupée
gd_data = get_gdistr(data)
# Affichage
print(gd_data){'toto': (11, 0.55), 'titi': (3, 0.15), 'tata': (6, 0.3)}Vous pouvez aussi utiliser la fonction suivante pour afficher une distribution groupée :
# Fonction pour un plus chouette affichage
def pprint_gd(gd):
mod_max_size = max([len(str(m)) for m in gd.keys()]+[len("Modalité")])
eff_max_size = max([len(str(gd[m][0])) for m in gd.keys()]+[len("Effectif")])
freq_max_size = max([len(str(gd[m][1])) for m in gd.keys()]+[len("Fréquence")])
print('-'*(mod_max_size+3+eff_max_size+3+freq_max_size+3))
print("Modalité".ljust(mod_max_size+3,' ')+"Effectif".rjust(eff_max_size+3,' ')+"Fréquence".rjust(freq_max_size+3,' '))
print('-'*(mod_max_size+3+eff_max_size+3+freq_max_size+3))
for k in gd.keys():
print(str(k).ljust(mod_max_size+3,' ')+str(gd[k][0]).rjust(eff_max_size+3,' ')+str(gd[k][1]).rjust(freq_max_size+3,' '))
return Nonepprint_gd(gd_data)----------------------------------
Modalité Effectif Fréquence
----------------------------------
toto 11 0.55
titi 3 0.15
tata 6 0.3Un autre exemple :
# Générons des données aléatoires (des float arrondis à 10^-2 entre 0 et 20)
import random
data = [round(random.random()*20,2) for _ in range(10)]
print("Données initiales : ",data,"\n")
data2 = cut(dat=data, split=[0,5,10,15,20])
print("Données dicrétisées : ",data2,"\n")
print("Tableau de la distribution groupée :")
pprint_gd(get_gdistr(data2))Données initiales : [14.14, 16.51, 1.56, 17.44, 11.01, 13.74, 19.17, 4.69, 7.42, 11.81]
Données dicrétisées : ['(10,15]', '(15,20]', '(0,5]', '(15,20]', '(10,15]', '(10,15]', '(15,20]', '(0,5]', '(5,10]', '(10,15]']
Tableau de la distribution groupée :
----------------------------------
Modalité Effectif Fréquence
----------------------------------
(10,15] 4 0.4
(15,20] 3 0.3
(5,10] 1 0.1
(0,5] 2 0.2Pour étudier la distribution d’une série associée à variable quantitative, on dispose d’un peu plus d’outils.
On a d’abord des indicateurs de position :
Ces indicateurs permettent de positionner les valeurs de la série dans l’espace des valeurs possibles.
Puis des indicateurs de dispersion :
Ces indicateurs traduisent la variabilité des valeurs.
Un couple d’indicateurs de position et de dispersion permet de résumer sommairement une série statistique quantitative.
[facultatif] Il existe aussi des indicateurs de forme qui permettent de quantifier l’asymétrie et l’aplatissement d’une distribution :
Exercice CALCUL DES INDICATEURS
Écrire les fonctions associées à ces indicateurs :
mean(dat)quantile(dat,p) (si vous n’avez jamais vu cette notion,
reportez-vous à cet
article wikipedia pour en comprendre le calcul -prendre de
préférence la formule « Fonction de distribution empirique avec mise à
la moyenne »)median(dat) (on pourra réutiliser
quantile(dat,0.5))stdev(dat)cofvar(dat)valrange(dat)iquarange(dat)Exemple :
# Génération de données aléatoires
import random
data = [round(random.random()*20,2) for _ in range(25)]
# Affichage des inficateurs
print("Moyenne : ",round(mean(data),2))
print("Médiane : ",round(median(data),2))
print("Écart-type : ",round(stdev(data),2))
print("Coef. de var. : ",round(cofvar(data),2))
print("Étendue : ",round(valrange(data),2))
print("Éc. interquart. : ",round(iquarange(data),2))
print("Prem. quartile : ",round(quantile(data,0.25),2))
print("Trois. quartile : ",round(quantile(data,0.75),2))Moyenne : 10.28
Médiane : 9.97
Écart-type : 5.54
Coef. de var. : 0.54
Étendue : 17.83
Éc. interquart. : 9.41
Prem. quartile : 5.48
Trois. quartile : 14.89En bref INDICATEURS
Pour résumer la distribution des valeurs observées pour une variable on dispose :
La représentation graphique la plus répandue et la plus efficace pour représenter une distribution statistique groupée est le diagramme à barre. Dans le cas d’une variable quantitative continue discrétisée, les barres sont « collées » (puisque les intervalles sont contigüs) et on parle alors d’histogramme. Chaque barre associée à une classe ou une modalité et proportionnelle à l’effectif ou la fréquence associée. Par soucis d’objectivité, il est important que le bas de chaque barre commence à 0.
On peut également utiliser un diagramme à secteurs (ce bon vieux camembert) mais son utilisation est, plus encore que le diagramme à barre, sujete à la « subjectivité » voire à la manipulation.
Nous allons utiliser le module matplotlib pour les
premières représentations graphiques.
import matplotlib.pyplot as plt
# Si vous voulez augmenter la qualité des images produites :
plt.rcParams['figure.dpi']= 300Préparons un jeu de données d’illustration :
# Données de test
data = ["toto","toto","tata","toto","titi",
"toto","tata","tata","toto","toto",
"toto","toto","titi","toto","titi",
"tata","toto","tata","tata","toto"]
# Extraction de la distribution groupée
data_gd = get_gdistr(data)Production d’un diagramme à barres :
# On récupère les modalités
classes = list(data_gd.keys())
# On récupère les effectifs pour s'en servir comme hauteurs des barres
heights = [data_gd[c][0] for c in classes]
# Production du barplot
plt.figure()
plt.bar(classes,heights)
plt.title("Effectifs de titi toto tata")
plt.xlabel("Modalité")
plt.ylabel("Effectif")
# Affichage
plt.show()Cette fois avec les fréquences relatives :
# On récupère les fréquences pour s'en servir comme hauteurs des barres
heights = [data_gd[c][1] for c in classes]
# Production du barplot
plt.figure()
plt.bar(classes,heights)
plt.title("Proportions de titi toto tata")
plt.xlabel("Modalité")
plt.ylabel("Fréquence")
# Affichage
plt.show()Toujours pour les variables qualitatives, il est possible de produire un diagramme à secteurs :
# On récupère les fréquences dans le tableau de la distribution groupé
props = [data_gd[c][1] for c in classes]
# PRoduction du graphique
plt.figure()
plt.title('Répartition des effectifs\n\n\n')
plt.pie(props, labels=classes,
autopct='%.0f%%',
radius=1.5)
# Affichage
plt.show()Pour les variables quantitatives, on dispose de la représentation en histogramme, qui finalement revient à discrétiser la variable puis à faire un diagramme à barres (en « collant » les barres) avec les modalités obtenues (les intervalles contigüs qui découpent l’espace des valeurs, qu’on appellera classes). Le nombre de barres de l’histogramme et leur largeur sont donc variables et dépendent de la discrétisation de la variable. La hauteur des barres représente, au choix, les effectifs des classes, ou les fréquences.
En général on choisit des classes d’amplitudes (largeurs) égales. Dans le cas contraire, il est préférable de représenter la fréquence par la surface des barres plutôt que par leur hauteur.
Attention : la fonction hist() de
matplotlib effectue la discrétisation toute seule.
Créons un jeu de données aléatoires pour illustrer :
# Génération de 59 notes aléatoires entre 0 et 20
data = [round(random.random()*20,2) for _ in range(50)]
print(data)[11.37, 7.44, 3.05, 14.45, 14.36, 14.1, 14.29, 1.29, 9.86, 12.65, 18.47, 6.46, 4.65, 12.24, 11.77, 6.66, 15.86, 2.46, 3.62, 16.14, 4.15, 16.42, 0.17, 19.26, 11.68, 5.19, 2.06, 14.25, 2.76, 10.6, 14.86, 2.9, 10.15, 10.01, 11.52, 10.03, 6.73, 1.85, 5.28, 9.53, 19.83, 1.45, 15.82, 16.51, 12.71, 3.62, 4.93, 10.57, 9.13, 17.68]et produisons un histogramme :
# Production de l'histogramme
# Ke second argument est la liste des "coupes" utilisées pour la discrétisation
# On peut fournir à la pkace, le nombre de barres (nombre d'intervalles)
plt.figure()
plt.hist(data, [0,2,4,6,8,10,12,14,16,18,20])
plt.title("Distribution des valeurs")
plt.ylabel("Effectif")
plt.xlabel("Valeur")
plt.show()Deuxième exemple :
# Production de l'histogramme
# Ke second argument est la liste des "coupes" utilisées pour la discrétisation
# On peut fournir à la pkace, le nombre de barres (nombre d'intervalles)
plt.figure()
plt.hist(data, 5)
plt.title("Distribution des valeurs")
plt.ylabel("Effectif")
plt.xlabel("Valeur")
plt.show()Enfin, il est difficile de ne pas parler d’une représentation old school mais qui s’avèrera très pratique par la suite : la boîte à moustaches. Cette représentation utilise quelques indicateurs (vus précédemment) pour proposer une vision synthétique de la distribution.
Exemple (sur les données précédentes) :
# Production du boxplot
fig = plt.figure()
plt.boxplot(data)
plt.grid()
# Affichage
plt.show()Pour « décrypter » une boite à moustaches, le schéma suivant est parfait (source : wikipedia « Boîte à moustaches ») :
En bref GRAPHIQUES
Pour résumer la distribution des valeurs observées pour une variable on dispose :
On peut évidemment personnaliser et améliorer ces représentations
(matplotlib permet de changer un grand nombre de
paramètres) ; il est également possible d’assembler les représentations
dans une seule image et de produire cette image dans un grand nombre de
formats.
plt.figure(figsize=(15, 6), dpi=120)
heights = [data_gd[c][0] for c in classes]
plt.style.use('default')
# subplot permet de diviser une figure en un tableau de sous-figures
# le premier argument est le nombre de lignes de ce tableau,
# le second le nombre de colonnes
# le troisième correspond au numéro de la cellule que l'on sélectionne
# ici :
# +---+---+
# | 1 | 2 |
# +---+---+
#
# Premier graphique
plt.subplot(1, 2, 1)
plt.bar(classes, heights)
plt.title("Proportions de titi toto tata")
plt.xlabel("Modalité")
plt.ylabel("Effectif")
# Second graphique
plt.subplot(1, 2, 2)
plt.bar(classes, heights, width = 0.3)
plt.title("Proportions de titi toto tata")
plt.xlabel("Modalité")
plt.ylabel("Effectif")
plt.grid(axis='y')
# Affichage
plt.show()Il est aussi possible de changer le style
globalement en utilisant les style sheets de
matplotlib :
# Changement de style pour l'ensemble des graphiques à venir
plt.style.use('dark_background')
plt.figure(figsize=(15, 6), dpi=120)
plt.subplot(1, 2, 1)
plt.bar(classes, heights)
plt.title("Proportions de titi toto tata")
plt.xlabel("Modalité")
plt.ylabel("Effectif")
plt.subplot(1, 2, 2)
plt.bar(classes, heights, width = 0.3)
plt.title("Proportions de titi toto tata")
plt.xlabel("Modalité")
plt.ylabel("Effectif")
plt.grid(axis='y')
plt.show()
# Restaurer le style pour les graphiques suivants
plt.style.use('default')
plt.rcParams["figure.dpi"] = 300A large share of ink on a graphic should present data-information, the ink changing as the data change. Data-ink is the non-erasable core of a graphic, the non-redundant ink arranged in response to variation in the numbers represented. (Edward Tüfte, 2001. The Visual Display of Quantitative Information)
Edward Tufte, légende de la visualisation de données, a beaucoup étudié l’impact des choix « graphiques » faits lors de la création d’une visualisation sur la perception qu’en a le lecteur.
Parmi de nombreux autres principes, il a notamment établi celui du ratio encre utilisée pour les données / quantité totale d’encre utilisée pour le graphique. D’après Tüfte, ce ratio doit être le plus élevé possible. Il estime en effet que les seuls élements graphiques qui doivent être affichés, sont ceux qui ne peuvent être effacés sans faire perdre du sens à la visu.
Bien que discutable, ce principe a le mérite de remettre au centre des préoccupations la question essentielle : « Qu’est-ce qu’on veut voir/montrer ?». En corrolaire, il permet d’éliminer toutes les « distractions » visuelles biaisant la peception du lecteur.
À l’opposé des principes de Tüfte, on trouve les très modernes « infographies », qu’on qualifie volontiers de « chartjunk ». Votre moteur de recherche préféré vous donnera rapidement un échantillon de ce qui se fait de pire… Mais on y renviendra dans les activités suivantes.
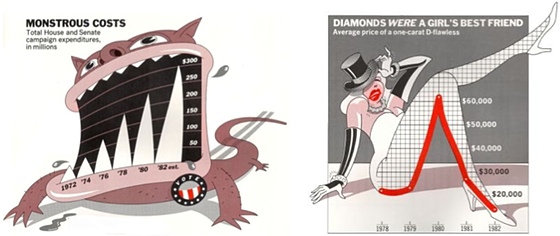
Exercice GRAPHIQUES TROMPEURS
Les graphiques suivants posent de sérieux problèmes de représentation. Après avoir identifié les entourloupes, proposer une représentation plus raisonnable (en supposant que les valeurs indiquées sont justes).
Les données disponibles ont généralement été prétraitées, voire transformées. Ainsi, on trouve fréquemment des données quantitatives sous forme de séries groupées. Cette transformation (discrétisation), correspond à une perte irréversible d’information.
Exercice DONNÉES GROUPÉES ET PERTE D’INFORMATION
Supposons que l’on dispose des données suivantes concernant les notes d’une promo :
# Dictionnaire contenant les données groupées
# clé : (a,b) ---> intervalle de note ]a,b] (sauf pour le premier où le 0 est inclus)
# valeur : n ---> nombre de notes comprises dans l'intervalle
data = {(0,5): 18,
(5,10): 7,
(10,15):13,
(15,20):10}Calculer la note moyenne à partir de ces données groupées (on prendra le centre de l’intervalle pour le calcul)
Voici les données brutes, avant regroupement :
data = [2.8, 2.9, 2.9, 3.1, 3.2, 3.4, 3.4, 3.5, 3.6, 3.8, 4.0, 4.0, 4.1, 4.3,
4.5, 4.7, 4.8, 4.8, 7.9, 8.2, 8.6, 8.7, 9.3, 9.4, 9.6, 12.8, 13.0,
13.1, 13.2, 13.2, 13.4, 13.7, 13.8, 13.9, 14.1, 14.1, 14.2, 14.7, 17.8,
18.1, 18.9, 19.0, 19.1, 19.1, 19.3, 19.6, 19.7, 19.9]Vérifier que la discrétisation puis le regroupement correspondent bien à ce qui était donné avant. Puis calculer la moyenne.
Qu’observe-t-on ?
Exercice MOYENNE OU MÉDIANE ?
On a relevé les salaires dans un micro-pays fictif.
salaires_A = [1243, 1278, 120124, 1394, 1296, 1289, 1303, 1083, 1291, 1337,
1075, 1361, 1259, 1138, 1188, 1217, 1164, 1535, 1283, 1275,
1146, 1196, 1237, 1191, 1389, 1210, 1067, 1094, 1249, 1239,
1262, 1294, 1360, 1276, 1208, 1234, 1091, 1306, 1089, 1148,
1185, 1192, 1186, 1075, 1057, 1221, 1291, 1421, 120099, 1348,
1089, 1171, 1290, 1071, 1235, 1202, 1304, 120118, 1396, 1293,
1280, 1225, 1237, 1297, 1242, 120029, 1179, 1115, 1105, 1146,
120044, 1296, 1268, 1288, 1102, 1123, 1308, 1244, 1099, 1147,
1098, 1406, 1275, 1206, 1377, 1243, 1152, 1138, 1205, 1132,
1221, 1370, 1328, 1138, 1279, 1081, 1109, 1316, 1291, 1213,
1159, 119901, 1148, 1090, 1288, 1234, 1241, 120016, 1326,
1165, 119917, 1148, 119949, 1133, 1019, 1212, 119925, 1281,
1367, 1102, 1241, 1188, 1281, 1389, 1092, 1163, 1227, 1191,
1228, 1056, 1106, 1151, 1162, 1229, 1334, 1243, 119959, 1208,
1177, 1217, 1133, 1364, 1147, 119931, 1149, 1211, 1181, 1213,
1389, 1199, 1249, 1291, 1137, 1055, 1211, 1307, 1141, 1098,
1048, 1238, 1071, 1277, 120116, 120047]Calculer le salaire moyen, puis le salaire médian. Qu’en penser ?
Dans le pays voisin, les salaires sont un peu différents :
salaires_B = [119965, 1217, 1124, 1379, 1129, 120063, 119930, 1104, 120120, 1348, 120128,
1226, 1173, 120024, 120032, 119862, 120056, 1305, 119902, 120098, 1166, 1180,
1061, 119816, 119929, 1226, 119944, 119847, 120094, 1089, 1298, 1103, 1205,
119782, 119904, 119875, 119954, 120162, 1322, 120031, 1100, 1123, 990, 120020,
119851, 120098, 1121, 120070, 1372, 1299, 119926, 1192, 119870, 120020, 1293,
120003, 1242, 1343, 119999, 1063, 120056, 1306, 1230, 119825, 1308, 1289, 1172,
1122, 120096, 120014, 1358, 1248, 120010, 1137, 1184, 120202, 1088, 119818,
120066, 1103, 1109, 1259, 1323, 119762, 1113, 1152, 119969, 119783, 119934,
1220, 119896, 120023, 119893, 120191, 1219, 120027, 119874, 120152, 1337]Calculer le salaire moyen et le salaire médian. Qu’observe-t-on ?
Visualiser les distributions des salaires dans chaque pays.
Proposer un résumé de ces deux séries.
Nous avons vu qu’on pouvait discrétiser une variable quantitative continue en remplaçant une valeur pas sa classe. On peut également changer ces valeurs en d’autres valeurs numériques continues.
Ces transformations permettent de changer l’échelle des valeurs et leur distribution.
La transformation logarithmique permet de changer l’échelle des valeurs d’une variable lorsqu’une minorité d’entre elles sont très élevées apr rapport aux autres. Elle consiste tout bêtement à remplacer chaque valeur (strictement positive) par son logarithme.
Exercice LOGARITHME
On a récupéré les données suivantes :
data = [1.65, 3.67, 1.96, 0.77, 0.45, 2.25, 0.47, 7.93, 0.77, 1.01,
0.53, 0.31, 0.25, 0.55, 0.14, 0.27, 4.05, 3.11, 0.27, 1.27,
2.33, 9.81, 1.07, 0.02, 0.55, 1.93, 0.09, 2.35, 6.16, 0.05,
0.02, 7.17, 11.55, 3.21, 1.36, 7.97, 0.3, 1.82, 2.0, 0.02,
2.12, 1.02, 0.49, 0.17, 0.03, 2.36, 0.08, 0.51, 0.09, 0.94,
2.71, 0.29, 8.55, 0.47, 10.14, 1.04, 2.01, 0.39, 1.07, 1.64,
4.23, 2.11, 0.08, 0.1, 0.01, 1.5, 7.66, 0.07, 0.37, 2.75,
1.64, 0.84, 0.01, 0.3, 2.97, 6.28, 0.29, 0.02, 0.03, 4.68,
0.61, 5.73, 1.08, 5.03, 8.55, 1.52, 4.55, 0.47, 0.28, 0.39,
1.16, 1.3, 0.08, 1.96, 0.76, 0.21, 0.43, 6.64, 7.05, 0.01]Qu’observe-t-on ?
La transformation en rangs consiste à remplacer chaque valeur par le rang qu’elle occupe dans la série triée. Cette transformation a pour intérêt de nous affranchir des écarts entre les valeurs.
Exercice RANGS
Écrire une fonction to_ranks(data) qui retourne
les rangs des valeurs de data. Autrement dit, cette
fonction retourne une liste dont le ième élément est le rang
de la valeur data[i] dans sorted_data (si
sorted_data est la liste issue du tri de data
dans l’ordre croissant).
Exemple de comportement attendu de la fonction :
to_ranks([3,8,1,11,7,4])[2, 5, 1, 6, 4, 3]On a récupéré les données suivantes :
data = [9.4531, 11.6358, 11.0114, 13.6833, 22.5199, 6.9069, 9.6858, 10.1612, 9.6639, 13.7164,
-0.1524, 9.3856, 5.6784, 12.4886, 4.4473, 9.5456, 10.3225, 13.1786, 13.4331, 5.8983,
9.9682, 9.1689, 8.3763, 8.3065, 11.2544, 3.9533, 13.1199, 9.8712, 9.3393, 10.1274,
8.3552, 14.1878, 4.4704, 6.5326, 14.853, 12.9896, 16.5132, 6.4729, 14.0004, 16.0347,
7.4854, 10.9724, 8.6938, 14.3512, 13.6721, 12.412, 16.6542, 7.3041, 17.4611, 10.977,
7.8374, 13.8277, 4.136, 5.4403, 11.4788, 10.3844, 14.0403, 5.1948, 3.6954, 8.7836,
7.0702, 9.4915, 13.9402, 9.4944, 12.3044, 12.7221, 14.4586, 11.0558, 12.657, 13.5342,
14.2622, 8.9576, 12.7594, 16.9846, 18.5019, 6.4132, 7.3614, 13.0121, 10.0488, 5.572,
8.7635, 7.2641, 12.6194, 16.1174, 6.9511, 9.6203, 12.4084, 10.3873, 10.1446, 13.3794,
9.9577, 10.2323, 7.4461, 8.7361, 15.8436, 9.0257, 13.1165, 10.529, 7.8485, 8.843]Qu’observe-t-on ?
[facultatif]
Comparez les temps d’exécution de votre fonction avec celle de
scipy (rankdata) :
import scipy.stats as sp
import random
import time
def compare(f1, f2, size, rep):
s_dtf1 = [0.0] * rep
s_dtf2 = [0.0] * rep
for i in range(rep) :
data = [random.random()] * size
t1 = time.time()
data2 = f1(data)
t2 = time.time()
s_dtf1[i] = t2 - t1
t1 = time.time()
data2 = f2(data)
t2 = time.time()
s_dtf2[i] = t2 - t1
print(f"Première fonction : \n temps moyen : {mean(s_dtf1)} (écart-type : {stdev(s_dtf1)}")
print(f"Deuxième fonction : \n temps moyen : {mean(s_dtf2)} (écart-type : {stdev(s_dtf2)}")
return None
compare(to_ranks, sp.rankdata, 100000, 100)Première fonction :
temps moyen : 0.008912229537963867 (écart-type : 0.00027077684329241536
Deuxième fonction :
temps moyen : 0.008651432991027832 (écart-type : 0.0004919407862603445Le centrage et la réduction consistent, respectivement, à retrancher à chaque valeur la moyenne de la série, et à les diviser par l’écart-type de la série. Cette transformation permet notamment de comparer des variables, en ramenant leurs valeurs dans des échalles comparables. Concrètement, la variable obtenue a ensuite une moyenne nulle et un écart-type de 1 (respectivement)
Exercice NORMALISATION
On a pu obtenir les notes au module de statistiques de l’année dernière :
data = [6.6, 8.9, 11.6, 5.5, 7.8, 13.3, 14.7, 6.8, 8.8, 19.5,
14.1, 9.7, 10.4, 11.0, 15.2, 16.4, 15.4, 13.3, 9.2, 10.7,
9.4, 11.8, 13.2, 15.9, 12.3, 15.6, 12.0, 5.7, 18.7, 15.6,
13.7, 16.2, 6.9, 13.4, 15.3, 21.0, 11.5, 17.8, 13.5, 15.5,
10.8, 18.0, 0.0, 9.4, 12.7, 12.4, 16.0, 4.2, 16.2, 3.5,
9.8, 11.6, 15.3, 8.9, 9.5, 16.8, 10.8, 15.2, 11.0, 11.3,
11.5, 13.7, 11.1, 19.3, 20.9, 7.9, 9.7, 11.4, 9.8, 18.7,
14.3, 17.3, 9.9, 16.6, 11.2, 19.0, 13.7, 13.8, 17.9, 9.6,
16.7, 19.7, 10.1, 9.4, 13.9, 5.0, 16.1, 10.9, 9.9, 14.0,
5.0, 7.9, 25.6, 11.6, 15.2, 15.7, 11.4, 5.8, 16.0, 14.2]Calculer la moyenne et l’écart-type de cette série.
Afficher un histogramme adapté.
Écrire une fonction scale(data, center, scale) qui
centre ou réduit une série contenue dans data (les
arguments center et scale sont des booléens
indiquant respectivement si les données doivent être centrées ou
réduites).
Exemple d’utilisation :
scale([0,1,2,3,4,5,6,7,8,9], center=True, scale=False)[-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]scale([0,1,2,3,4,5,6,7,8,9], center=True, scale=True)[-1.5666989036012806,
-1.2185435916898848,
-0.8703882797784892,
-0.5222329678670935,
-0.17407765595569785,
0.17407765595569785,
0.5222329678670935,
0.8703882797784892,
1.2185435916898848,
1.5666989036012806]Synthèse
À l’issue de cette activité pratique vous devez être capable de choisir et d’interpréter avec sagacité, les principaux outils graphiques et numériques permettant de résumer la distribution d’une variable.
Pour clore ce premier sujet, vous allez reproduire les calculs à l’aide d’un tableur (ici LibreOffice Calc).