Partie 3 Les graphes from scratch
Bien qu’il existe de nombreuses bibliothèques permettant de créer, manipuler et étudier les graphes, il peut être intéressant de construire à la main ces outils. Le graphe est un support pédagogique simple qui permet de consolider les bases algorithmiques. Il ne nécessite pas de structures de données complexes ni d’outils mathématiques pointus.
3.1 Implémentation simple
Comme le présente Claude Berge 3, un graphe est un ensemble de points et un ensemble de flèches dont chacune relie deux points.
Mathématiquement, un graphe4 \(G\) est donc un couple \((V,E)\) où :
- \(V\) est un ensemble (des sommets du graphes)
- \(E\) est un ensemble de couples de \(V\) (les arcs du graphes)
On peut aussi voir \(E\) comme une relation binaire sur \(V\).
D’un point de vue informatique on dispose de plusieurs représentations des graphes5 parmi lesquelles :
- la matrice d’ajacence,
- les listes d’arcs,
- les listes de successeurs.
Dans ce document, nous choisissons la matrice d’adjacence comme représentation des graphes.
3.2 Matrice d’adjacence
Soit \(G=(V,E)\) un graphe contenant \(n\) sommets et \(p\) arcs. On définit la matrice d’adjacence \(M\) de \(G\) par :
\[M = (m_{i,j})_{\substack{i=1,...,n\\j=1,...,n}}\]
avec :
\[ \forall i \in \{1,\ldots,n\}, \forall j \in \{1,\ldots,n\}, \left\{ \begin{array}{lll} m_{i,j} & = & 1 \quad \text{ si }(i,j)\in E,\\ m_{i,j} & = & 0 \quad \text{ sinon} \end{array}\right. \]
En python le plus simple est d’utiliser le type array de la bibliothèque numpy pour implémenter une matrice d’adjacence6 :
import numpy as np
M = np.array([[0,0,1,1],
[1,1,0,0],
[0,1,0,1],
[1,0,1,0]])
print(M)## [[0 0 1 1]
## [1 1 0 0]
## [0 1 0 1]
## [1 0 1 0]]Pour la visualisation d’un graphe à partir d’une matrice d’adjacence, on utilisera la fonction de rendu du module networkx et celle d’affichage de matplotlib.
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
nx.draw(nx.DiGraph(M))
plt.show()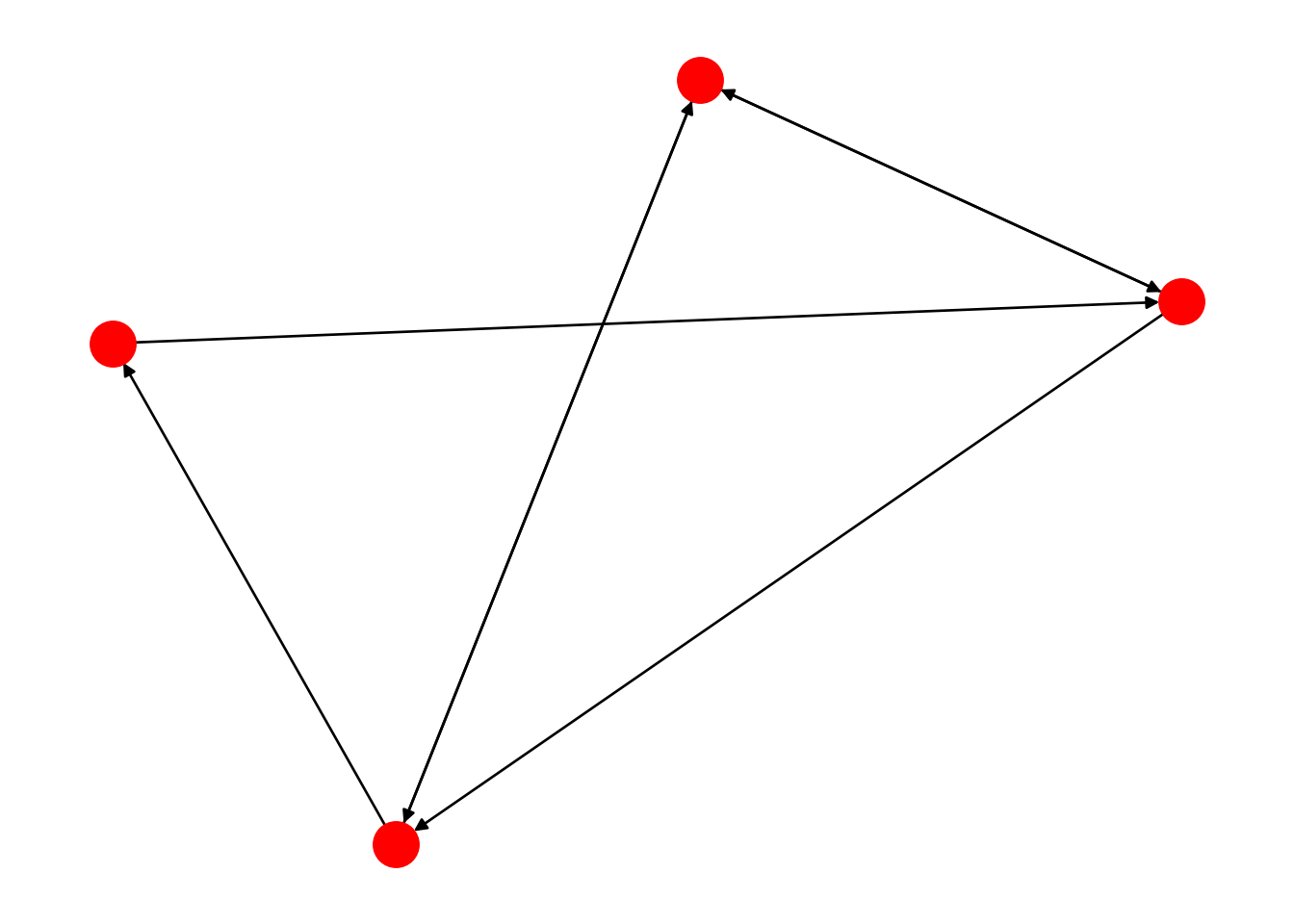
La fonction draw() possède de nombreuses options de personnalisation :
options = {
'node_color' : 'yellow',
'node_size' : 550,
'edge_color' : 'tab:grey',
'with_labels': True
}
G = nx.DiGraph(M)
plt.figure()
nx.draw(G, **options)
plt.show()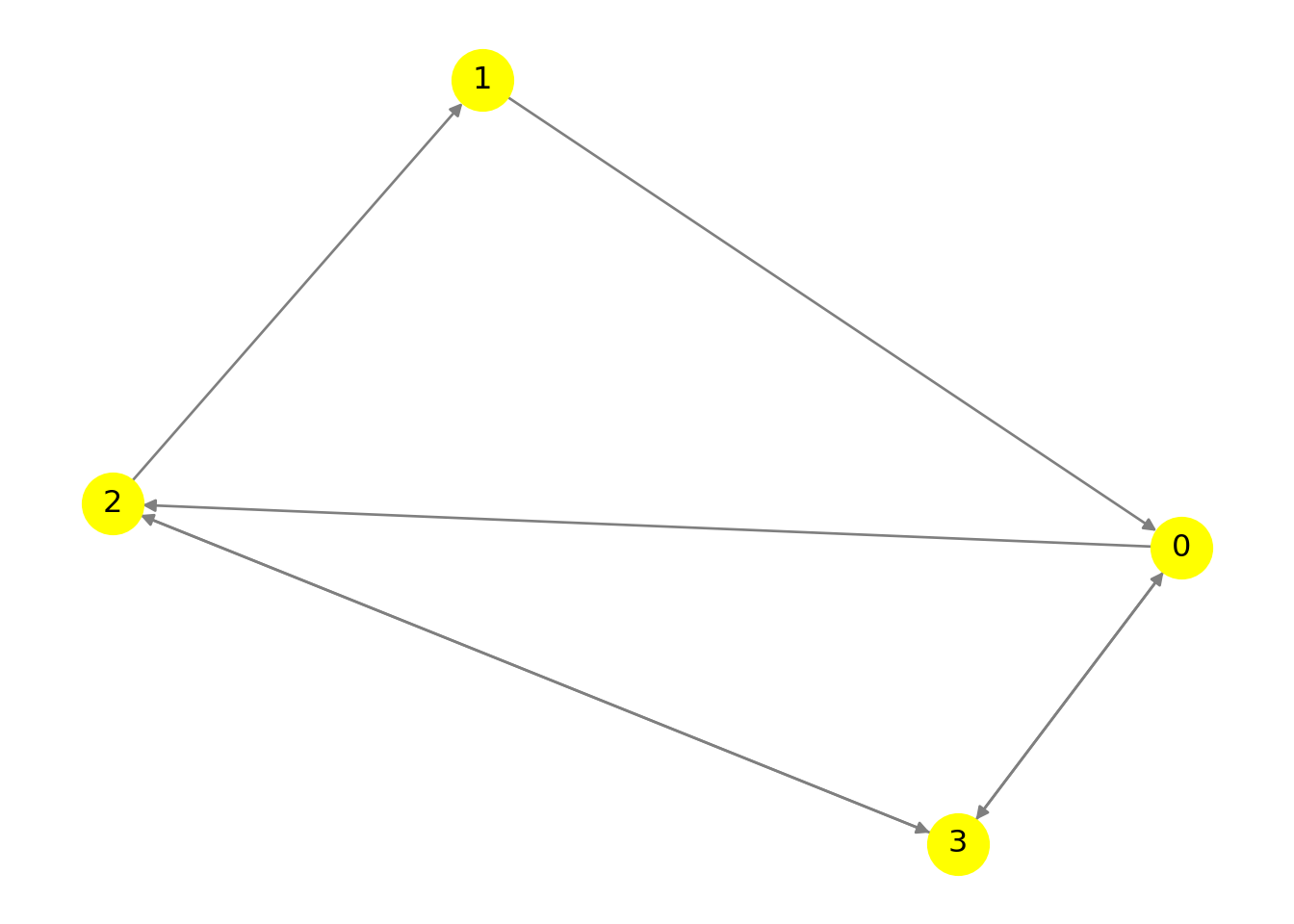
Pour les graphes valués (i.e. dont les arcs portent des valeurs numériques), on pourra utiliser le même principe, en remplaçant, les \(1\) par les valeurs portées par les arcs et en représentant l’absence d’arc par \(+\infty\)7.
inf = float("inf")
M = np.array([[inf, inf, 1, 2],
[ 3, 8, inf, inf],
[inf, 11, inf, 1],
[ -2, inf, 1, inf]])
print(M)## [[inf inf 1. 2.]
## [ 3. 8. inf inf]
## [inf 11. inf 1.]
## [-2. inf 1. inf]]La représentation de la structure du graphe étant faite, on peut choisir de n’utiliser que la matrice d’adjacence.
Mais on peut aussi définir une struture de données contenant toutes les informations spécifiant le graphe 8 :
- la matrice d’adjacence ou de poids,
- l’information d’orientation,
- l’information de pondération des arcs,
On peut assembler ces données dans un dictionnaire qui définira le graphe :
G = {
'matrix' : np.array([[0, 1, 0, 1], # Matrice d'adjacence
[1, 1, 1, 0],
[0, 0, 0, 1],
[1, 1, 0, 0]]),
'directed': True, # Orientation
'weighted': False, # Valuation des arcs
}Affichage :
def display(G, options = None):
if G['weighted']:
M = (G['matrix'] < inf)*1
else:
M = G['matrix']
if G['directed']:
G2 = nx.DiGraph(M)
else:
G2 = nx.Graph(M)
plt.figure()
if(options != None):
nx.draw(G2, **options)
else:
options = {
'node_color' : 'yellow',
'node_size' : 550,
'edge_color' : 'tab:grey',
'with_labels': True
}
nx.draw(G2,**options)
plt.show()
display(G)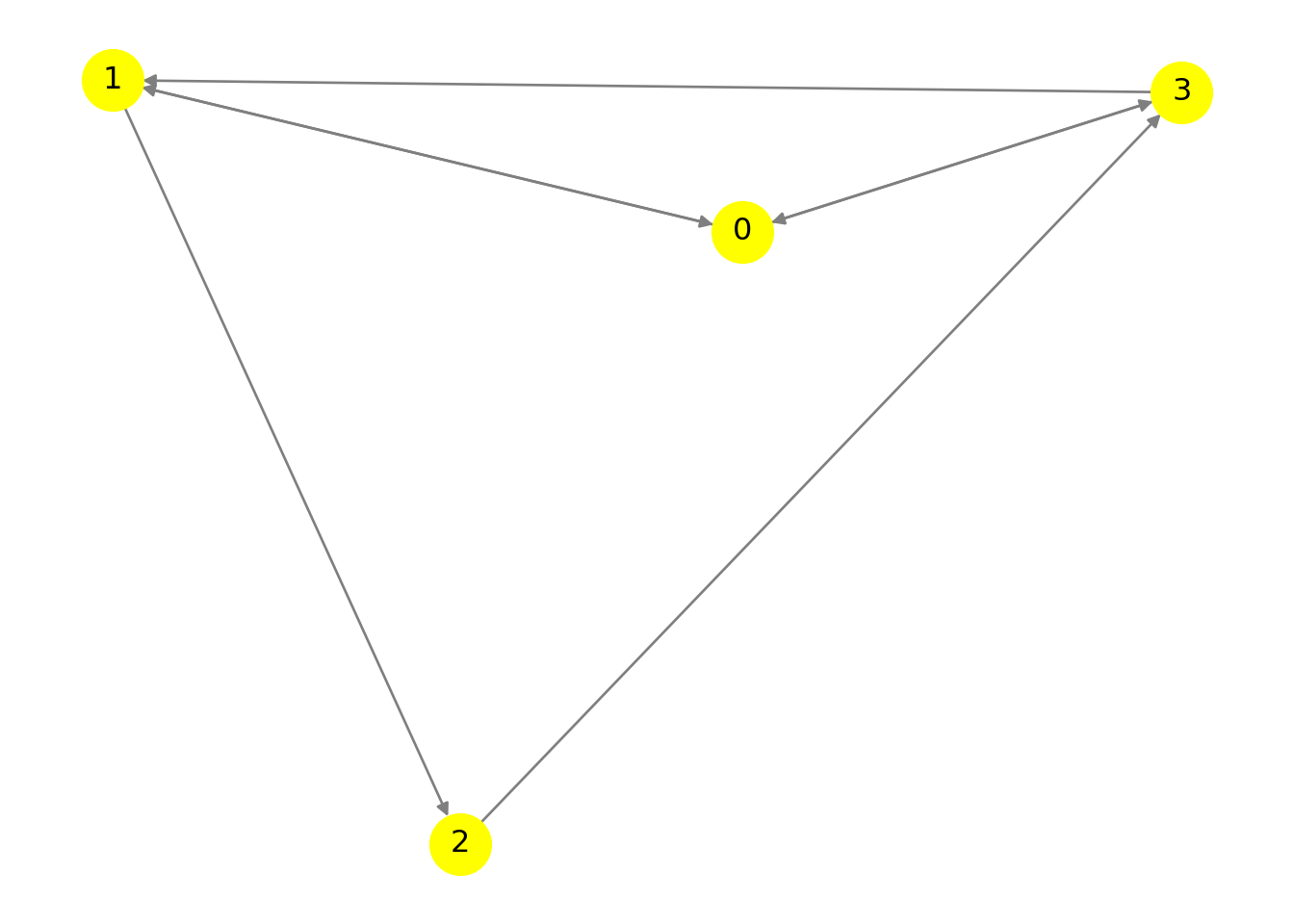
3.3 Fonctions basiques
La mise en place d’algorithmes de graphes nécessite de disposer de quelques fonctions basiques afin de simplifier leur écriture :
successeurs(G,i)qui détermine la liste des sucesseurs d’un sommet \(i\) dans le graphe \(G\),predecesseurs(G,i)qui détermine la liste des prédécesseurs d’un sommet \(i\) dans le graphe \(G\),voisins(G,i)qui détermine la liste des voisins d’un sommet \(i\) dans le graphe \(G\),degreExt(G,i)qui retourne le demi-degré extérieur du sommet \(i\) dans \(G\)degreInt(G,i)qui retourne le demi-degré intérieur du sommet \(i\) dans \(G\)degre(G,i)qui retourne le degré du sommet \(i\) dans \(G\)
# Liste des sucesseurs d'un sommet
def successeurs(g,i) :
M = g['matrix']
directed = g['directed']
weighted = g['weighted']
n = np.shape(M)[0]
listeSuccesseurs = []
for j in range(0 if directed else i,n) :
if weighted :
if M[i,j] < inf:
listeSuccesseurs = listeSuccesseurs + [j]
else :
if M[i,j] == 1 :
listeSuccesseurs = listeSuccesseurs + [j]
return(listeSuccesseurs)
# Liste des prédecesseurs d'un somemt
def predecesseurs(g,i) :
M = g['matrix']
directed = g['directed']
weighted = g['weighted']
n = np.shape(M)[0]
listePredecesseurs = []
for j in range(0 if directed else i,n) :
if weighted :
if M[j,i] < inf:
listePredecesseurs = listePredecesseurs + [j]
else :
if M[j,i] == 1 :
listePredecesseurs = listePredecesseurs + [j]
return(listePredecesseurs)
# Liste des voisins d'un sommet
def voisins(g,i) :
s = successeurs(g,i)
p = predecesseurs(g,i)
return(list(set().union(s,p)))
# Degres
def degreExt(g,i):
return(len(successeurs(g,i)))
def degreInt(g,i):
return(len(predecesseurs(g,i)))
def degre(g,i):
if (g['directed']):
deg = len(successeurs(g,i)) + len(predecesseurs(g,i))
else :
deg = len(voisins(g,i))
return(deg)Testons ces fonctions sur le graphe defini plus haut :
print(G['matrix'])## [[0 1 0 1]
## [1 1 1 0]
## [0 0 0 1]
## [1 1 0 0]]print(successeurs(G,2)) # Successeurs du sommet C (indice 2)## [3]print(degreExt(G,2)) # Demi-degré extérieur du sommet C (indice 2)## 1print(predecesseurs(G,2)) # Prédécesseurs du sommet C (indice 2)## [1]print(degreInt(G,2)) # Demi-degré intérieur du sommet C (indice 2)## 1print(voisins(G,2)) # Voisins du sommet C (indice 2)## [1, 3]print(degre(G,2)) # Degré du sommet C (indice 2)## 2print(degre(G,1)) # Degré du sommet B (indice 1)## 6Ces primitives sont suffisantes pour implémenter un grand nombre d’algorithmes.
3.4 Parcours de graphes
Nous allons implémenter les deux parcours, « en largeur d’abord » et « en profondeur d’abord ».
Parcours « en largeur d’abord »
Dans ce parcours le principe est d’utiliser une file d’attente pour stocker les successeurs à « visiter »
def BFS(G,s) :
visited = [] # liste des sommets visité
marked = [s] # liste des sommets marqués
queue = [s] # file d'attente
while(len(queue)!=0) :
e = queue[0]
queue = queue[1:]
for t in successeurs(G,e) :
if t not in marked :
queue = queue + [t]
marked = marked + [t]
visited = visited + [e]
return(visited)Test :
print(BFS(G,3))## [3, 0, 1, 2]Parcours « en profondeur d’abord »
En utlisant une pile, écrire la fonction DFS(G,s) qui parcourt \(G\) « en profondeur d’abord » à partir de \(s\).
def DFS(G,s) :
visited = [] # liste des sommets visité
marked = [s] # liste des sommets marqués
stack = [s] # pile
#
# TODO
#3.5 Pagerank « maison »
Nous allons implémenter une version simple de l’algorithme du pagerank.
Le principe est le suivant : en simulant le comportement d’un « surfeur aléatoire » sur un réseau de \(n\) pages web (les sommets du graphe) liées entre elles par des liens hypertextes (les arcs) on obtient des probabilités d’arrivée sur les pages qui définissent les scores de pagerank.
On représente la position d’un « surfeur aléatoire » à l’aide d’une suite de vecteurs stochastiques \((u_t)_{t\in\mathbb{N}}\) avec \(u_0\) sa position initiale. On appelle \(T\) la matrice de transition telle que :
\(T_{i,j}\) est la probabilité de passage de la page \(j\) à la page \(i\).
On a donc, matriciellement :
\[u_{t+1} = T\times u_{t}\]
def pagerank(G):
# Matrice d'adjacence
M = np.copy(G['matrix'])
n = np.shape(M)[0]
# Transformation en matrice de transition
M = np.transpose(M) # Transposition de la matrice d'adjacence
M = M.astype(float) # Transtypage int --> float
for i in range(0,n):
s = 0
for j in range(0,n):
s = s + M[j,i]
if s == 0:
M[i,i] = 1
else:
for j in range(0,n):
M[j,i] = M[j,i] / s
# Initialisation de la marche aléatoire
u0 = np.transpose(np.array([[1./n]*n])) # initialisation proba
u1 = M @ u0 # première transition
# Répétition jusqu'à convergence
while(sum((u1-u0)*(u1-u0))>0.0001):
u0 = np.copy(u1)
u1 = M @ u1
# Fin
return(u1)Test :
print(pagerank(G))## [[0.25203082]
## [0.37576089]
## [0.12515003]
## [0.24705826]]Adapter la fonction précédente afin d’éviter l’effet « trou noir » en permettant à chaque itération, de passer à n’importe quel sommet du graphe, de manière équiprobable. Il s’agit donc de perturber la marche aléatoire avec un « saut » de probabilité \(\alpha \in [0,1]\).
Matriciellement :
\[u_{n+1} = \alpha\left(\begin{array}{c} 1/n \\ \vdots \\ 1/n \end{array}\right) + (1-\alpha) T \times u_{n}\]
def pagerank2(G,alpha=0.05):
# Matrice d'adjacence
M = np.copy(G['matrix'])
n = np.shape(M)[0]
# Transformation en matrice de transition
M = np.transpose(M)
M = M.astype(float)
for i in range(0,n):
s = 0
for j in range(0,n):
s = s + M[j,i]
if s == 0:
M[i,i] = 1
else:
for j in range(0,n):
M[j,i] = M[j,i] / s
#
# TODO
#Remerciements : Grégory Arganini, Étienne Coutant, Didier Gillard, Antoine Jonquet et Olivier Nocent pour les relectures, conseils, avis et tests.
Claude Berge, Graphes et hypergrapĥes, Dunod, 1970↩
par « graphe » on entend \(1-\)graphe, c’est-à-dire un graphe dans lequel, pour chaque couple de sommet \((i,j)\) il n’existe pas plus d’un arc de \(i\) vers \(j\).↩
il existe d’autres représentations qui sont souvent des déclinaisons de celles-ci.↩
nous avons choisi les valeurs \(0\) et \(1\) plutôt que des booléens pour rester proche de la définition mathématique d’une part, et pour bénéficier des opérations sur les entiers d’autre part.↩
En
python, on représente l’infini de la manière suivante :inf = float("inf")↩en se contentant de prendre la matrice d’adjacence, on simplifie la gestion de graphe, mais on complique les prototypes des fonctions primitives.↩